JAX integration

This notebook introduces the use of JAX with tlm_adjoint.

JAX can be used e.g. with the Firedrake backend as an escape-hatch, allowing custom operations to be implemented using lower level code. However it can also be used independently, without a finite element code generator. Here JAX is used with tlm_adjoint to implement and differentiate a finite difference code.

Forward problem

We consider the diffusion equation in the unit square domain, subject to homogeneous Dirichlet boundary conditions,

\[\partial_t u = \kappa \left( \partial_{xx} + \partial_{yy} \right) u + m \left( x, y \right) \qquad \text{on} ~ \left( x, y \right) \in \left( 0, 1 \right)^2,\]

\[u = 0 \qquad \text{on} ~ \partial \Omega.\]

This is discretized using a basic finite difference scheme, using second order centered finite differencing for the \(x\) and \(y\) dimensions and forward Euler for the \(t\) dimension.

Here we implement the discretization using JAX, for \(\kappa = 0.01\), \(t \in \left[ 0, 0.25 \right]\), a time step size of \(0.0025\), and a uniform grid with a grid spacing of \(0.02\). We consider the case where \(m \left( x, y \right) = 0\), and compute the \(L^4\) norm of the \(t = T\) solution (with the \(L^4\) norm defined via nearest neighbour interpolation of the finite difference solution, ignoring boundary points where the solution is zero).

%matplotlib inline

import matplotlib.pyplot as plt
import jax

jax.config.update("jax_enable_x64", True)

N = 50
kappa = 0.01
T = 0.25
N_t = 100

dx = 1.0 / N
dt = T / N_t


x = jax.numpy.linspace(0.0, 1.0, N + 1)
y = jax.numpy.linspace(0.0, 1.0, N + 1)
X, Y = jax.numpy.meshgrid(x, y, indexing="ij")


def timestep(x_n, m):
    x_np1 = jax.numpy.zeros_like(x_n)
    x_np1 = x_np1.at[1:-1, 1:-1].set(
        x_n[1:-1, 1:-1]
        + (kappa * dt / (dx * dx)) * (x_n[1:-1, 2:]
                                      + x_n[:-2, 1:-1]
                                      - 4.0 * x_n[1:-1, 1:-1]
                                      + x_n[2:, 1:-1]
                                      + x_n[1:-1, :-2])
        + dt * m[1:-1, 1:-1])
    return x_np1


def functional(x_n):
    x_n = x_n.reshape((N + 1, N + 1))
    return (dx * dx * (x_n[1:-1, 1:-1] ** 4).sum()) ** 0.25


def forward(x_0, m):
    x_n = x_0.copy()
    for _ in range(N_t):
        x_n = timestep(x_n, m)
    J = functional(x_n)
    return x_n, J


x_0 = jax.numpy.zeros((N + 1, N + 1), dtype=jax.numpy.double)
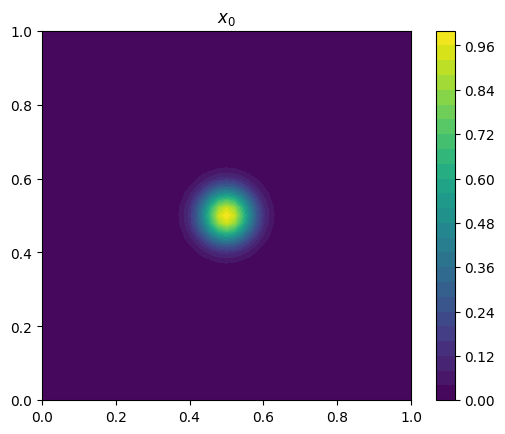
x_0 = x_0.at[1:-1, 1:-1].set(jax.numpy.exp(-((X[1:-1, 1:-1] - 0.5) ** 2 + (Y[1:-1, 1:-1]- 0.5) ** 2) / (2.0 * (0.05 ** 2))))
m = jax.numpy.zeros((N + 1, N + 1), dtype=jax.numpy.double)

fig, ax = plt.subplots(1, 1)
p = ax.contourf(x, y, x_0.T, 32)
fig.colorbar(p)
ax.set_aspect(1.0)
ax.set_title("$x_0$")

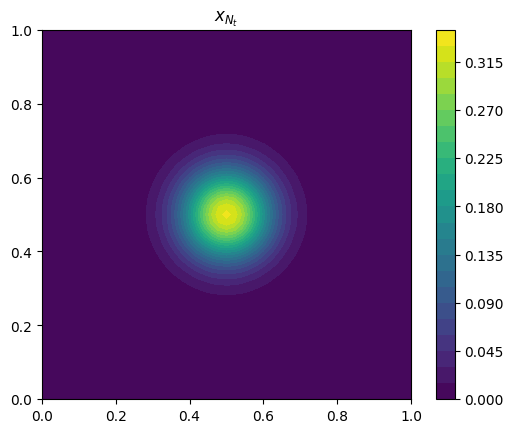
x_n, J = forward(x_0, m)
print(f"{J=}")

fig, ax = plt.subplots(1, 1)
p = ax.contourf(x, y, x_n.T, 32)
fig.colorbar(p)
ax.set_aspect(1.0)
ax.set_title("$x_{N_t}$")

J=Array(0.11009761, dtype=float64)

Text(0.5, 1.0, '$x_{N_t}$')

Adding tlm_adjoint

The tlm_adjoint Vector class wraps ndim 1 JAX arrays. The following uses the tlm_adjoint call_jax function to record JAX operations on the internal tlm_adjoint manager. Note the use of new_block, indicating steps, and enabling use of a step-based checkpointing schedule.

from tlm_adjoint import *

import jax

jax.config.update("jax_enable_x64", True)
reset_manager()

N = 50
kappa = 0.01
T = 0.25
N_t = 100

dx = 1.0 / N
dt = T / N_t


x = jax.numpy.linspace(0.0, 1.0, N + 1)
y = jax.numpy.linspace(0.0, 1.0, N + 1)
X, Y = jax.numpy.meshgrid(x, y, indexing="ij")


def timestep(x_n, m):
    x_n = x_n.reshape((N + 1, N + 1))
    m = m.reshape((N + 1, N + 1))
    x_np1 = jax.numpy.zeros_like(x_n)
    x_np1 = x_np1.at[1:-1, 1:-1].set(
        x_n[1:-1, 1:-1]
        + (kappa * dt / (dx * dx)) * (x_n[1:-1, 2:]
                                      + x_n[:-2, 1:-1]
                                      - 4.0 * x_n[1:-1, 1:-1]
                                      + x_n[2:, 1:-1]
                                      + x_n[1:-1, :-2])
        + dt * m[1:-1, 1:-1])
    return x_np1.flatten()


def functional(x_n):
    x_n = x_n.reshape((N + 1, N + 1))
    return (dx * dx * (x_n[1:-1, 1:-1] ** 4).sum()) ** 0.25


def forward(x_0, m):
    x_n = Vector((N + 1) ** 2)
    x_np1 = Vector((N + 1) ** 2)
    x_n.assign(x_0)
    for n_t in range(N_t):
        call_jax(x_np1, (x_n, m), timestep)
        x_n.assign(x_np1)
        if n_t < N_t - 1:
            new_block()
    J = new_jax_float()
    call_jax(J, x_n, functional)
    return J


x_0 = jax.numpy.zeros((N + 1, N + 1), dtype=jax.numpy.double)
x_0 = x_0.at[1:-1, 1:-1].set(jax.numpy.exp(-((X[1:-1, 1:-1] - 0.5) ** 2 + (Y[1:-1, 1:-1]- 0.5) ** 2) / (2.0 * (0.05 ** 2))))
x_0 = Vector(x_0.flatten())
m = Vector((N + 1) ** 2)

start_manager()
J = forward(x_0, m)
stop_manager()

(True, True)

We can now verify first order tangent-linear and adjoint calculations, and a second order reverse-over-forward calculation, using Taylor remainder convergence tests. Here we consider derivatives with respect to \(m\).

min_order = taylor_test_tlm(lambda m: forward(x_0, m), m, tlm_order=1)
assert min_order > 1.99

min_order = taylor_test_tlm_adjoint(lambda m: forward(x_0, m), m, adjoint_order=1)
assert min_order > 1.99

min_order = taylor_test_tlm_adjoint(lambda m: forward(x_0, m), m, adjoint_order=2)
assert min_order > 1.99

Error norms, no tangent-linear   = [4.98147223e-04 2.48932094e-04 1.24430787e-04 6.22065920e-05
 3.11010973e-05]
Orders,      no tangent-linear   = [1.00081994 1.00040876 1.00020411 1.00010199]
Error norms, with tangent-linear = [5.64828623e-07 1.40896441e-07 3.51881408e-08 8.79272075e-09
 2.19765236e-09]
Orders,      with tangent-linear = [2.00317803 2.00147398 2.00070773 2.00034646]
Error norms, no adjoint   = [5.50056001e-04 2.74881388e-04 1.37404160e-04 6.86929601e-05
 3.43442017e-05]
Orders,      no adjoint   = [1.00076928 1.00038354 1.00019152 1.0000957 ]
Error norms, with adjoint = [5.85211095e-07 1.45992502e-07 3.64622824e-08 9.11127658e-09
 2.27729418e-09]
Orders,      with adjoint = [2.00306284 2.0014175  2.00067976 2.00033253]
Error norms, no adjoint   = [1.09370953e-04 5.44944701e-05 2.72042039e-05 1.35919447e-05
 6.79350872e-06]
Orders,      no adjoint   = [1.00504789 1.00228023 1.00107773 1.00052309]
Error norms, with adjoint = [7.13419081e-07 1.65703320e-07 3.98205198e-08 9.75295966e-09
 2.41287403e-09]
Orders,      with adjoint = [2.10614729 2.05701855 2.02960006 2.01508749]