Time-dependent example

This notebook describes the calculation of derivative information for a time-dependent problem using tlm_adjoint with the Firedrake backend. Overheads associated with building the records of calculations are discussed, and a checkpointing schedule is applied.

The binomial checkpointing schedule is based on the method described in:

• Andreas Griewank and Andrea Walther, ‘Algorithm 799: revolve: an implementation of checkpointing for the reverse or adjoint mode of computational differentiation’, ACM Transactions on Mathematical Software, 26(1), pp. 19–45, 2000, doi: 10.1145/347837.347846

Forward problem

We consider the solution of a linear time-dependent partial differential equation, followed by the calculation of the square of the \(L^2\)-norm of the final time solution. We assume real spaces and a real build of Firedrake throughout.

Specifically we consider the advection-diffusion equation in two dimensions, in the form

\[\partial_t u + \partial_x \psi \partial_y u - \partial_y \psi \partial_x u = \kappa \left( \partial_{xx} + \partial_{yy} \right) u,\]

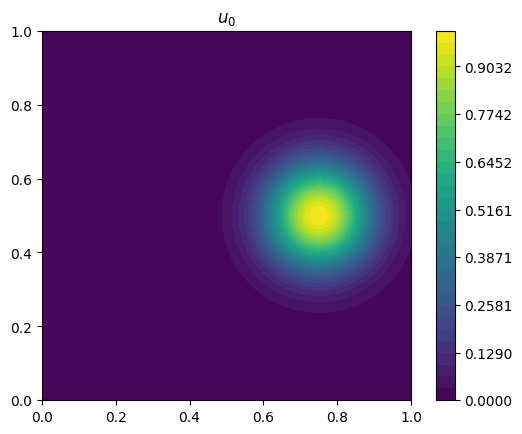
where \(\psi\) vanishes on the domain boundary, and subject to zero flux boundary conditions. We consider the spatial domain \(\left( x, y \right) \in \left( 0, 1 \right)^2\) and temporal domain \(t \in \left[ 0, 0.1 \right]\), with \(\psi \left( x, y \right) = -\sin \left( \pi x \right) \sin \left( \pi y \right)\) and \(\kappa = 0.01\), and an initial condition \(u \left( x, y, t=0 \right) = \exp \left[ -50 \left( \left( x - 0.75 \right)^2 + \left( y - 0.5 \right)^2 \right) \right]\).

The problem is discretized using \(P_1\) continuous finite elements to represent both the solution \(u\) at each time level and the stream function \(\psi\). The problem is discretized in time using the implicit trapezoidal rule.

A simple implementation in Firedrake takes the form:

%matplotlib inline

from firedrake import *
from firedrake.pyplot import tricontourf

import matplotlib.pyplot as plt
import numpy as np

T = 0.1
N = 100
dt = Constant(T / N)

mesh = UnitSquareMesh(128, 128)
X = SpatialCoordinate(mesh)
space = FunctionSpace(mesh, "Lagrange", 1)
test = TestFunction(space)
trial = TrialFunction(space)

psi = Function(space, name="psi")
psi.interpolate(-sin(pi * X[0]) * sin(pi * X[1]))

kappa = Constant(0.01)

u_0 = Function(space, name="u_0")
u_0.interpolate(exp(-50.0 * ((X[0] - 0.75) ** 2 + (X[1] - 0.5) ** 2)))

u_n = Function(space, name="u_n")
u_np1 = Function(space, name="u_np1")

u_h = 0.5 * (u_n + trial)
F = (inner(trial - u_n, test) * dx
     + dt * inner(psi.dx(0) * u_h.dx(1) - psi.dx(1) * u_h.dx(0), test) * dx
     + dt * inner(kappa * grad(u_h), grad(test)) * dx)
lhs, rhs = system(F)

problem = LinearVariationalProblem(
    lhs, rhs, u_np1,
    constant_jacobian=True)
solver = LinearVariationalSolver(
    problem, solver_parameters={"ksp_type": "preonly",
                                "pc_type": "lu"})

u_n.assign(u_0)
for n in range(N):
    solver.solve()
    u_n.assign(u_np1)

J = assemble(inner(u_n, u_n) * dx)


def plot_output(u, title):
    r = (u.dat.data_ro.min(), u.dat.data_ro.max())
    eps = (r[1] - r[0]) * 1.0e-12
    p = tricontourf(u, np.linspace(r[0] - eps, r[1] + eps, 32))
    plt.gca().set_title(title)
    plt.colorbar(p)
    plt.gca().set_aspect(1.0)


plot_output(u_0, title="$u_0$")
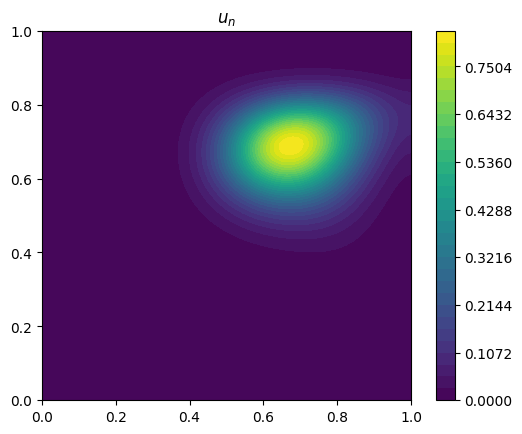
plot_output(u_n, title="$u_n$")

Adding tlm_adjoint

We first modify the code so that tlm_adjoint processes the calculations:

from firedrake import *
from tlm_adjoint.firedrake import *

reset_manager("memory", {})

T = 0.1
N = 100
dt = Constant(T / N)

mesh = UnitSquareMesh(128, 128)
X = SpatialCoordinate(mesh)
space = FunctionSpace(mesh, "Lagrange", 1)
test = TestFunction(space)
trial = TrialFunction(space)

psi = Function(space, name="psi")
psi.interpolate(-sin(pi * X[0]) * sin(pi * X[1]))

kappa = Constant(0.01)

u_0 = Function(space, name="u_0")
u_0.interpolate(exp(-50.0 * ((X[0] - 0.75) ** 2 + (X[1] - 0.5) ** 2)))


def forward(u_0, psi):
    u_n = Function(space, name="u_n")
    u_np1 = Function(space, name="u_np1")

    u_h = 0.5 * (u_n + trial)
    F = (inner(trial - u_n, test) * dx
         + dt * inner(psi.dx(0) * u_h.dx(1) - psi.dx(1) * u_h.dx(0), test) * dx
         + dt * inner(kappa * grad(u_h), grad(test)) * dx)
    lhs, rhs = system(F)

    problem = LinearVariationalProblem(
        lhs, rhs, u_np1,
        constant_jacobian=True)
    solver = LinearVariationalSolver(
        problem, solver_parameters={"ksp_type": "preonly",
                                    "pc_type": "lu"})

    u_n.assign(u_0)
    for n in range(N):
        solver.solve()
        u_n.assign(u_np1)

    J = Functional(name="J")
    J.assign(inner(u_n, u_n) * dx)
    return J


start_manager()
J = forward(u_0, psi)
stop_manager()

(True, True)

Later we will configure a checkpointing schedule. Resetting the manager resets the record of forward equations but does not reset the checkpointing configuration, and so in this example whenever we reset the manager we also return it to the default checkpointing configuration with reset_manager("memory", {}).

Computing derivatives using an adjoint

The compute_gradient function can be used to compute derivatives using the adjoint method. Here we compute the derivative of the square of the \(L^2\)-norm of the final timestep solution, considered a function of the control defined by the initial condition u_0 and stream function psi, with respect to this control:

dJ_du_0, dJ_dpsi = compute_gradient(J, (u_0, psi))

As a simple check of the result, note that the solution to the (discretized) partial differential equation is unchanged by the addition of a constant to the stream function. Hence we expect the directional derivative with respect to the stream function, with direction equal to the unity valued function, to be zero. This is indeed found to be the case (except for roundoff errors):

one = Function(space, name="one")
one.interpolate(Constant(1.0))

dJ_dpsi_one = assemble(action(dJ_dpsi, one))

print(f"{dJ_dpsi_one=}")

assert abs(dJ_dpsi_one) < 1.0e-17

dJ_dpsi_one=3.50741757937361e-18

Computing Hessian information using an adjoint of a tangent-linear

We next compute a Hessian action. Although the following calculation does work, it is inefficient – you may wish to skip forward to the optimized calculations.

Here we compute a ‘mixed’ Hessian action, by defining a directional derivative with respect to the stream function, and then differentiating this with respect to the initial condition:

from firedrake import *
from tlm_adjoint.firedrake import *

reset_manager("memory", {})

T = 0.1
N = 100
dt = Constant(T / N)

mesh = UnitSquareMesh(128, 128)
X = SpatialCoordinate(mesh)
space = FunctionSpace(mesh, "Lagrange", 1)
test = TestFunction(space)
trial = TrialFunction(space)

psi = Function(space, name="psi")
psi.interpolate(-sin(pi * X[0]) * sin(pi * X[1]))

kappa = Constant(0.01)

u_0 = Function(space, name="u_0")
u_0.interpolate(exp(-50.0 * ((X[0] - 0.75) ** 2 + (X[1] - 0.5) ** 2)))


def forward(u_0, psi):
    u_n = Function(space, name="u_n")
    u_np1 = Function(space, name="u_np1")

    u_h = 0.5 * (u_n + trial)
    F = (inner(trial - u_n, test) * dx
         + dt * inner(psi.dx(0) * u_h.dx(1) - psi.dx(1) * u_h.dx(0), test) * dx
         + dt * inner(kappa * grad(u_h), grad(test)) * dx)
    lhs, rhs = system(F)

    problem = LinearVariationalProblem(
        lhs, rhs, u_np1,
        constant_jacobian=True)
    solver = LinearVariationalSolver(
        problem, solver_parameters={"ksp_type": "preonly",
                                    "pc_type": "lu"})

    u_n.assign(u_0)
    for n in range(N):
        solver.solve()
        u_n.assign(u_np1)

    J = Functional(name="J")
    J.assign(inner(u_n, u_n) * dx)
    return J


zeta = Function(space, name="zeta")
zeta.assign(psi)
configure_tlm((psi, zeta))

start_manager()
J = forward(u_0, psi)
stop_manager()

dJ_dpsi_zeta = var_tlm(J, (psi, zeta))

d2J_dpsi_zeta_du_0 = compute_gradient(dJ_dpsi_zeta, u_0)

Optimization

In the above we have successfully built a record of calculations, and used this to compute derivative information. However there are two issues:

1. Building the record has a noticable cost – the forward calculation has slowed down. In the second order calculation overheads associated with the tangent-linear lead to substantial additional costs.

2. tlm_adjoint records the solution of the partial differential equation on all time levels. The memory usage here is manageable. However memory limits will be exceeded for larger problems with more fields, spatial degrees of freedom, or timesteps.

Let’s fix these issues in order.

Optimizing the annotation

In the above code tlm_adjoint builds a new record for each finite element variational problem it encounters. Even though only one LinearVariationalSolver is instantiated, an EquationSolver record is instantiated on each call to the solve method. Building the record is sufficiently expensive that the forward calculation noticeably slows down, and this also leads to significant extra processing in the derivative calculations.

Instead we can instantiate an EquationSolver directly, and reuse it. However if we do only that then the code will still be inefficient. A single EquationSolver will be used, but new linear solver data will be constructed each time its solve method is called. We need to also apply an optimization analogous to the constant_jacobian=True argument supplied to LinearVariationalProblem.

A simple fix is to add cache_jacobian=True when instantiating the EquationSolver:

eq = EquationSolver(
    lhs == rhs, u_np1,
    solver_parameters={"ksp_type": "preonly",
                       "pc_type": "lu"},
    cache_jacobian=True)

This works, but we can instead let tlm_adjoint detect that linear solver data can be cached. We can do that by adding static=True when instantiating variables whose value is unchanged throughout the forward calculation:

from firedrake import *
from tlm_adjoint.firedrake import *

reset_manager("memory", {})
clear_caches()

T = 0.1
N = 100
dt = Constant(T / N, static=True)

mesh = UnitSquareMesh(128, 128)
X = SpatialCoordinate(mesh)
space = FunctionSpace(mesh, "Lagrange", 1)
test = TestFunction(space)
trial = TrialFunction(space)

psi = Function(space, name="psi", static=True)
psi.interpolate(-sin(pi * X[0]) * sin(pi * X[1]))

kappa = Constant(0.01, static=True)

u_0 = Function(space, name="u_0", static=True)
u_0.interpolate(exp(-50.0 * ((X[0] - 0.75) ** 2 + (X[1] - 0.5) ** 2)))


def forward(u_0, psi):
    u_n = Function(space, name="u_n")
    u_np1 = Function(space, name="u_np1")

    u_h = 0.5 * (u_n + trial)
    F = (inner(trial - u_n, test) * dx
         + dt * inner(psi.dx(0) * u_h.dx(1) - psi.dx(1) * u_h.dx(0), test) * dx
         + dt * inner(kappa * grad(u_h), grad(test)) * dx)
    lhs, rhs = system(F)

    eq = EquationSolver(
        lhs == rhs, u_np1,
        solver_parameters={"ksp_type": "preonly",
                           "pc_type": "lu"})

    u_n.assign(u_0)
    for n in range(N):
        eq.solve()
        u_n.assign(u_np1)

    J = Functional(name="J")
    J.assign(inner(u_n, u_n) * dx)
    return J


start_manager()
J = forward(u_0, psi)
stop_manager()

(True, True)

If we now query the relevant tlm_adjoint caches:

print(f"{len(assembly_cache())=}")
print(f"{len(linear_solver_cache())=}")

assert len(assembly_cache()) == 2
assert len(linear_solver_cache()) == 1

len(assembly_cache())=2
len(linear_solver_cache())=1

we find that linear solver data associated with a single matrix has been cached. We also find that two assembled objects have been cached – it turns out that there are two cached matrices. As well as caching the matrix associated with the left-hand-side of the discrete problem, a matrix associated with the right-hand-side has been assembled and cached. Assembly of the right-hand-side has been converted into a matrix multiply. If we wished we could disable right-hand-side optimizations by adding cache_rhs_assembly=False:

eq = EquationSolver(
    lhs == rhs, u_np1,
    solver_parameters={"ksp_type": "preonly",
                       "pc_type": "lu"},
    cache_rhs_assembly=False)

Using a checkpointing schedule

To address the storage issue we enable checkpointing. Here we enable binomial checkpointing with storage of a maximum of \(10\) forward restart checkpoints in memory:

from firedrake import *
from tlm_adjoint.firedrake import *

import logging

logger = logging.getLogger("tlm_adjoint")
logger.setLevel(logging.DEBUG)
root_logger = logging.getLogger()
if len(logger.handlers) == 1:
    if len(root_logger.handlers) == 1:
        root_logger.handlers.pop()
    root_logger.addHandler(logger.handlers.pop())

reset_manager("memory", {})
clear_caches()

T = 0.1
N = 100
dt = Constant(T / N, static=True)

mesh = UnitSquareMesh(128, 128)
X = SpatialCoordinate(mesh)
space = FunctionSpace(mesh, "Lagrange", 1)
test = TestFunction(space)
trial = TrialFunction(space)

psi = Function(space, name="psi", static=True)
psi.interpolate(-sin(pi * X[0]) * sin(pi * X[1]))

kappa = Constant(0.01, static=True)

u_0 = Function(space, name="u_0", static=True)
u_0.interpolate(exp(-50.0 * ((X[0] - 0.75) ** 2 + (X[1] - 0.5) ** 2)))


def forward(u_0, psi):
    u_n = Function(space, name="u_n")
    u_np1 = Function(space, name="u_np1")

    u_h = 0.5 * (u_n + trial)
    F = (inner(trial - u_n, test) * dx
         + dt * inner(psi.dx(0) * u_h.dx(1) - psi.dx(1) * u_h.dx(0), test) * dx
         + dt * inner(kappa * grad(u_h), grad(test)) * dx)
    lhs, rhs = system(F)

    eq = EquationSolver(
        lhs == rhs, u_np1,
        solver_parameters={"ksp_type": "preonly",
                           "pc_type": "lu"})

    u_n.assign(u_0)
    for n in range(N):
        eq.solve()
        u_n.assign(u_np1)
        if n < N - 1:
            new_block()

    J = Functional(name="J")
    J.assign(inner(u_n, u_n) * dx)
    return J


configure_checkpointing("multistage", {"snaps_in_ram": 10, "blocks": N})
start_manager()
J = forward(u_0, psi)
stop_manager()

forward: forward advance to 9223372036854775807
forward: forward advance to 21
forward: save checkpoint data at 0 in RAM
forward: forward advance to 40
forward: save checkpoint data at 21 in RAM
forward: forward advance to 57
forward: save checkpoint data at 40 in RAM
forward: forward advance to 72
forward: save checkpoint data at 57 in RAM
forward: forward advance to 79
forward: save checkpoint data at 72 in RAM
forward: forward advance to 85
forward: save checkpoint data at 79 in RAM
forward: forward advance to 90
forward: save checkpoint data at 85 in RAM
forward: forward advance to 94
forward: save checkpoint data at 90 in RAM
forward: forward advance to 97
forward: save checkpoint data at 94 in RAM
forward: forward advance to 99
forward: save checkpoint data at 97 in RAM
forward: forward advance to 100

(True, True)

The key changes here are:

• Configuration of a checkpointing schedule using configure_checkpointing. Here binomial checkpointing is applied, with a maximum of \(10\) forward restart checkpoints stored in memory, indicated using the "snaps_in_ram" parameter. The total number of steps is indicated using the "blocks" parameter.

• The indication of the steps using new_block().

Extra logging output is also enabled so that we can see the details of the checkpointing schedule.

Computing derivatives

We are now ready to compute derivatives. However a key restriction is that we can, with this checkpointing schedule, only perform the adjoint calculation once per forward calculation. We cannot call compute_gradient a second time, without first rerunning the entire forward calculation.

In the following we compute both first and second derivative information using a single adjoint calculation:

from firedrake import *
from tlm_adjoint.firedrake import *

import logging

logger = logging.getLogger("tlm_adjoint")
logger.setLevel(logging.DEBUG)
root_logger = logging.getLogger()
if len(logger.handlers) == 1:
    if len(root_logger.handlers) == 1:
        root_logger.handlers.pop()
    root_logger.addHandler(logger.handlers.pop())

reset_manager("memory", {})
clear_caches()

T = 0.1
N = 100
dt = Constant(T / N, static=True)

mesh = UnitSquareMesh(128, 128)
X = SpatialCoordinate(mesh)
space = FunctionSpace(mesh, "Lagrange", 1)
test = TestFunction(space)
trial = TrialFunction(space)

psi = Function(space, name="psi", static=True)
psi.interpolate(-sin(pi * X[0]) * sin(pi * X[1]))

kappa = Constant(0.01, static=True)

u_0 = Function(space, name="u_0", static=True)
u_0.interpolate(exp(-50.0 * ((X[0] - 0.75) ** 2 + (X[1] - 0.5) ** 2)))


def forward(u_0, psi):
    u_n = Function(space, name="u_n")
    u_np1 = Function(space, name="u_np1")

    u_h = 0.5 * (u_n + trial)
    F = (inner(trial - u_n, test) * dx
         + dt * inner(psi.dx(0) * u_h.dx(1) - psi.dx(1) * u_h.dx(0), test) * dx
         + dt * inner(kappa * grad(u_h), grad(test)) * dx)
    lhs, rhs = system(F)

    eq = EquationSolver(
        lhs == rhs, u_np1,
        solver_parameters={"ksp_type": "preonly",
                           "pc_type": "lu"})

    u_n.assign(u_0)
    for n in range(N):
        eq.solve()
        u_n.assign(u_np1)
        if n < N - 1:
            new_block()

    J = Functional(name="J")
    J.assign(inner(u_n, u_n) * dx)
    return J


zeta_u_0 = ZeroFunction(space, name="zeta_u_0")
zeta_psi = Function(space, name="zeta_psi", static=True)
zeta_psi.assign(psi)
configure_tlm(((u_0, psi), (zeta_u_0, zeta_psi)))

configure_checkpointing("multistage", {"snaps_in_ram": 10, "blocks": N})
start_manager()
J = forward(u_0, psi)
stop_manager()

dJ_dpsi_zeta = var_tlm(J, ((u_0, psi), (zeta_u_0, zeta_psi)))

dJ_du_0, dJ_dpsi, d2J_dpsi_zeta_du_0 = compute_gradient(
    dJ_dpsi_zeta, (zeta_u_0, zeta_psi, u_0))

forward: forward advance to 9223372036854775807
forward: forward advance to 21
forward: save checkpoint data at 0 in RAM
forward: forward advance to 40
forward: save checkpoint data at 21 in RAM
forward: forward advance to 57
forward: save checkpoint data at 40 in RAM
forward: forward advance to 72
forward: save checkpoint data at 57 in RAM
forward: forward advance to 79
forward: save checkpoint data at 72 in RAM
forward: forward advance to 85
forward: save checkpoint data at 79 in RAM
forward: forward advance to 90
forward: save checkpoint data at 85 in RAM
forward: forward advance to 94
forward: save checkpoint data at 90 in RAM
forward: forward advance to 97
forward: save checkpoint data at 94 in RAM
forward: forward advance to 99
forward: save checkpoint data at 97 in RAM
forward: forward advance to 100
reverse: adjoint step back to 99
reverse: load checkpoint data at 97 from RAM and keep
reverse: forward advance to 98
reverse: forward advance to 99
reverse: adjoint step back to 98
reverse: load checkpoint data at 97 from RAM and delete
reverse: forward advance to 98
reverse: adjoint step back to 97
reverse: load checkpoint data at 94 from RAM and keep
reverse: forward advance to 95
reverse: forward advance to 96
reverse: save checkpoint data at 95 in RAM
reverse: forward advance to 97
reverse: adjoint step back to 96
reverse: load checkpoint data at 95 from RAM and delete
reverse: forward advance to 96
reverse: adjoint step back to 95
reverse: load checkpoint data at 94 from RAM and delete
reverse: forward advance to 95
reverse: adjoint step back to 94
reverse: load checkpoint data at 90 from RAM and keep
reverse: forward advance to 91
reverse: forward advance to 92
reverse: save checkpoint data at 91 in RAM
reverse: forward advance to 93
reverse: save checkpoint data at 92 in RAM
reverse: forward advance to 94
reverse: adjoint step back to 93
reverse: load checkpoint data at 92 from RAM and delete
reverse: forward advance to 93
reverse: adjoint step back to 92
reverse: load checkpoint data at 91 from RAM and delete
reverse: forward advance to 92
reverse: adjoint step back to 91
reverse: load checkpoint data at 90 from RAM and delete
reverse: forward advance to 91
reverse: adjoint step back to 90
reverse: load checkpoint data at 85 from RAM and keep
reverse: forward advance to 86
reverse: forward advance to 87
reverse: save checkpoint data at 86 in RAM
reverse: forward advance to 88
reverse: save checkpoint data at 87 in RAM
reverse: forward advance to 89
reverse: save checkpoint data at 88 in RAM
reverse: forward advance to 90
reverse: adjoint step back to 89
reverse: load checkpoint data at 88 from RAM and delete
reverse: forward advance to 89
reverse: adjoint step back to 88
reverse: load checkpoint data at 87 from RAM and delete
reverse: forward advance to 88
reverse: adjoint step back to 87
reverse: load checkpoint data at 86 from RAM and delete
reverse: forward advance to 87
reverse: adjoint step back to 86
reverse: load checkpoint data at 85 from RAM and delete
reverse: forward advance to 86
reverse: adjoint step back to 85
reverse: load checkpoint data at 79 from RAM and keep
reverse: forward advance to 80
reverse: forward advance to 81
reverse: save checkpoint data at 80 in RAM
reverse: forward advance to 82
reverse: save checkpoint data at 81 in RAM
reverse: forward advance to 83
reverse: save checkpoint data at 82 in RAM
reverse: forward advance to 84
reverse: save checkpoint data at 83 in RAM
reverse: forward advance to 85
reverse: adjoint step back to 84
reverse: load checkpoint data at 83 from RAM and delete
reverse: forward advance to 84
reverse: adjoint step back to 83
reverse: load checkpoint data at 82 from RAM and delete
reverse: forward advance to 83
reverse: adjoint step back to 82
reverse: load checkpoint data at 81 from RAM and delete
reverse: forward advance to 82
reverse: adjoint step back to 81
reverse: load checkpoint data at 80 from RAM and delete
reverse: forward advance to 81
reverse: adjoint step back to 80
reverse: load checkpoint data at 79 from RAM and delete
reverse: forward advance to 80
reverse: adjoint step back to 79
reverse: load checkpoint data at 72 from RAM and keep
reverse: forward advance to 73
reverse: forward advance to 74
reverse: save checkpoint data at 73 in RAM
reverse: forward advance to 75
reverse: save checkpoint data at 74 in RAM
reverse: forward advance to 76
reverse: save checkpoint data at 75 in RAM
reverse: forward advance to 77
reverse: save checkpoint data at 76 in RAM
reverse: forward advance to 78
reverse: save checkpoint data at 77 in RAM
reverse: forward advance to 79
reverse: adjoint step back to 78
reverse: load checkpoint data at 77 from RAM and delete
reverse: forward advance to 78
reverse: adjoint step back to 77
reverse: load checkpoint data at 76 from RAM and delete
reverse: forward advance to 77
reverse: adjoint step back to 76
reverse: load checkpoint data at 75 from RAM and delete
reverse: forward advance to 76
reverse: adjoint step back to 75
reverse: load checkpoint data at 74 from RAM and delete
reverse: forward advance to 75
reverse: adjoint step back to 74
reverse: load checkpoint data at 73 from RAM and delete
reverse: forward advance to 74
reverse: adjoint step back to 73
reverse: load checkpoint data at 72 from RAM and delete
reverse: forward advance to 73
reverse: adjoint step back to 72
reverse: load checkpoint data at 57 from RAM and keep
reverse: forward advance to 59
reverse: forward advance to 61
reverse: save checkpoint data at 59 in RAM
reverse: forward advance to 63
reverse: save checkpoint data at 61 in RAM
reverse: forward advance to 65
reverse: save checkpoint data at 63 in RAM
reverse: forward advance to 67
reverse: save checkpoint data at 65 in RAM
reverse: forward advance to 69
reverse: save checkpoint data at 67 in RAM
reverse: forward advance to 71
reverse: save checkpoint data at 69 in RAM
reverse: forward advance to 72
reverse: adjoint step back to 71
reverse: load checkpoint data at 69 from RAM and keep
reverse: forward advance to 70
reverse: forward advance to 71
reverse: adjoint step back to 70
reverse: load checkpoint data at 69 from RAM and delete
reverse: forward advance to 70
reverse: adjoint step back to 69
reverse: load checkpoint data at 67 from RAM and keep
reverse: forward advance to 68
reverse: forward advance to 69
reverse: adjoint step back to 68
reverse: load checkpoint data at 67 from RAM and delete
reverse: forward advance to 68
reverse: adjoint step back to 67
reverse: load checkpoint data at 65 from RAM and keep
reverse: forward advance to 66
reverse: forward advance to 67
reverse: adjoint step back to 66
reverse: load checkpoint data at 65 from RAM and delete
reverse: forward advance to 66
reverse: adjoint step back to 65
reverse: load checkpoint data at 63 from RAM and keep
reverse: forward advance to 64
reverse: forward advance to 65
reverse: adjoint step back to 64
reverse: load checkpoint data at 63 from RAM and delete
reverse: forward advance to 64
reverse: adjoint step back to 63
reverse: load checkpoint data at 61 from RAM and keep
reverse: forward advance to 62
reverse: forward advance to 63
reverse: adjoint step back to 62
reverse: load checkpoint data at 61 from RAM and delete
reverse: forward advance to 62
reverse: adjoint step back to 61
reverse: load checkpoint data at 59 from RAM and keep
reverse: forward advance to 60
reverse: forward advance to 61
reverse: adjoint step back to 60
reverse: load checkpoint data at 59 from RAM and delete
reverse: forward advance to 60
reverse: adjoint step back to 59
reverse: load checkpoint data at 57 from RAM and keep
reverse: forward advance to 58
reverse: forward advance to 59
reverse: adjoint step back to 58
reverse: load checkpoint data at 57 from RAM and delete
reverse: forward advance to 58
reverse: adjoint step back to 57
reverse: load checkpoint data at 40 from RAM and keep
reverse: forward advance to 42
reverse: forward advance to 44
reverse: save checkpoint data at 42 in RAM
reverse: forward advance to 46
reverse: save checkpoint data at 44 in RAM
reverse: forward advance to 48
reverse: save checkpoint data at 46 in RAM
reverse: forward advance to 50
reverse: save checkpoint data at 48 in RAM
reverse: forward advance to 52
reverse: save checkpoint data at 50 in RAM
reverse: forward advance to 54
reverse: save checkpoint data at 52 in RAM
reverse: forward advance to 56
reverse: save checkpoint data at 54 in RAM
reverse: forward advance to 57
reverse: adjoint step back to 56
reverse: load checkpoint data at 54 from RAM and keep
reverse: forward advance to 55
reverse: forward advance to 56
reverse: adjoint step back to 55
reverse: load checkpoint data at 54 from RAM and delete
reverse: forward advance to 55
reverse: adjoint step back to 54
reverse: load checkpoint data at 52 from RAM and keep
reverse: forward advance to 53
reverse: forward advance to 54
reverse: adjoint step back to 53
reverse: load checkpoint data at 52 from RAM and delete
reverse: forward advance to 53
reverse: adjoint step back to 52
reverse: load checkpoint data at 50 from RAM and keep
reverse: forward advance to 51
reverse: forward advance to 52
reverse: adjoint step back to 51
reverse: load checkpoint data at 50 from RAM and delete
reverse: forward advance to 51
reverse: adjoint step back to 50
reverse: load checkpoint data at 48 from RAM and keep
reverse: forward advance to 49
reverse: forward advance to 50
reverse: adjoint step back to 49
reverse: load checkpoint data at 48 from RAM and delete
reverse: forward advance to 49
reverse: adjoint step back to 48
reverse: load checkpoint data at 46 from RAM and keep
reverse: forward advance to 47
reverse: forward advance to 48
reverse: adjoint step back to 47
reverse: load checkpoint data at 46 from RAM and delete
reverse: forward advance to 47
reverse: adjoint step back to 46
reverse: load checkpoint data at 44 from RAM and keep
reverse: forward advance to 45
reverse: forward advance to 46
reverse: adjoint step back to 45
reverse: load checkpoint data at 44 from RAM and delete
reverse: forward advance to 45
reverse: adjoint step back to 44
reverse: load checkpoint data at 42 from RAM and keep
reverse: forward advance to 43
reverse: forward advance to 44
reverse: adjoint step back to 43
reverse: load checkpoint data at 42 from RAM and delete
reverse: forward advance to 43
reverse: adjoint step back to 42
reverse: load checkpoint data at 40 from RAM and keep
reverse: forward advance to 41
reverse: forward advance to 42
reverse: adjoint step back to 41
reverse: load checkpoint data at 40 from RAM and delete
reverse: forward advance to 41
reverse: adjoint step back to 40
reverse: load checkpoint data at 21 from RAM and keep
reverse: forward advance to 23
reverse: forward advance to 25
reverse: save checkpoint data at 23 in RAM
reverse: forward advance to 27
reverse: save checkpoint data at 25 in RAM
reverse: forward advance to 29
reverse: save checkpoint data at 27 in RAM
reverse: forward advance to 31
reverse: save checkpoint data at 29 in RAM
reverse: forward advance to 33
reverse: save checkpoint data at 31 in RAM
reverse: forward advance to 35
reverse: save checkpoint data at 33 in RAM
reverse: forward advance to 37
reverse: save checkpoint data at 35 in RAM
reverse: forward advance to 39
reverse: save checkpoint data at 37 in RAM
reverse: forward advance to 40
reverse: adjoint step back to 39
reverse: load checkpoint data at 37 from RAM and keep
reverse: forward advance to 38
reverse: forward advance to 39
reverse: adjoint step back to 38
reverse: load checkpoint data at 37 from RAM and delete
reverse: forward advance to 38
reverse: adjoint step back to 37
reverse: load checkpoint data at 35 from RAM and keep
reverse: forward advance to 36
reverse: forward advance to 37
reverse: adjoint step back to 36
reverse: load checkpoint data at 35 from RAM and delete
reverse: forward advance to 36
reverse: adjoint step back to 35
reverse: load checkpoint data at 33 from RAM and keep
reverse: forward advance to 34
reverse: forward advance to 35
reverse: adjoint step back to 34
reverse: load checkpoint data at 33 from RAM and delete
reverse: forward advance to 34
reverse: adjoint step back to 33
reverse: load checkpoint data at 31 from RAM and keep
reverse: forward advance to 32
reverse: forward advance to 33
reverse: adjoint step back to 32
reverse: load checkpoint data at 31 from RAM and delete
reverse: forward advance to 32
reverse: adjoint step back to 31
reverse: load checkpoint data at 29 from RAM and keep
reverse: forward advance to 30
reverse: forward advance to 31
reverse: adjoint step back to 30
reverse: load checkpoint data at 29 from RAM and delete
reverse: forward advance to 30
reverse: adjoint step back to 29
reverse: load checkpoint data at 27 from RAM and keep
reverse: forward advance to 28
reverse: forward advance to 29
reverse: adjoint step back to 28
reverse: load checkpoint data at 27 from RAM and delete
reverse: forward advance to 28
reverse: adjoint step back to 27
reverse: load checkpoint data at 25 from RAM and keep
reverse: forward advance to 26
reverse: forward advance to 27
reverse: adjoint step back to 26
reverse: load checkpoint data at 25 from RAM and delete
reverse: forward advance to 26
reverse: adjoint step back to 25
reverse: load checkpoint data at 23 from RAM and keep
reverse: forward advance to 24
reverse: forward advance to 25
reverse: adjoint step back to 24
reverse: load checkpoint data at 23 from RAM and delete
reverse: forward advance to 24
reverse: adjoint step back to 23
reverse: load checkpoint data at 21 from RAM and keep
reverse: forward advance to 22
reverse: forward advance to 23
reverse: adjoint step back to 22
reverse: load checkpoint data at 21 from RAM and delete
reverse: forward advance to 22
reverse: adjoint step back to 21
reverse: load checkpoint data at 0 from RAM and keep
reverse: forward advance to 2
reverse: forward advance to 4
reverse: save checkpoint data at 2 in RAM
reverse: forward advance to 6
reverse: save checkpoint data at 4 in RAM
reverse: forward advance to 8
reverse: save checkpoint data at 6 in RAM
reverse: forward advance to 10
reverse: save checkpoint data at 8 in RAM
reverse: forward advance to 12
reverse: save checkpoint data at 10 in RAM
reverse: forward advance to 14
reverse: save checkpoint data at 12 in RAM
reverse: forward advance to 16
reverse: save checkpoint data at 14 in RAM
reverse: forward advance to 18
reverse: save checkpoint data at 16 in RAM
reverse: forward advance to 20
reverse: save checkpoint data at 18 in RAM
reverse: forward advance to 21
reverse: adjoint step back to 20
reverse: load checkpoint data at 18 from RAM and keep
reverse: forward advance to 19
reverse: forward advance to 20
reverse: adjoint step back to 19
reverse: load checkpoint data at 18 from RAM and delete
reverse: forward advance to 19
reverse: adjoint step back to 18
reverse: load checkpoint data at 16 from RAM and keep
reverse: forward advance to 17
reverse: forward advance to 18
reverse: adjoint step back to 17
reverse: load checkpoint data at 16 from RAM and delete
reverse: forward advance to 17
reverse: adjoint step back to 16
reverse: load checkpoint data at 14 from RAM and keep
reverse: forward advance to 15
reverse: forward advance to 16
reverse: adjoint step back to 15
reverse: load checkpoint data at 14 from RAM and delete
reverse: forward advance to 15
reverse: adjoint step back to 14
reverse: load checkpoint data at 12 from RAM and keep
reverse: forward advance to 13
reverse: forward advance to 14
reverse: adjoint step back to 13
reverse: load checkpoint data at 12 from RAM and delete
reverse: forward advance to 13
reverse: adjoint step back to 12
reverse: load checkpoint data at 10 from RAM and keep
reverse: forward advance to 11
reverse: forward advance to 12
reverse: adjoint step back to 11
reverse: load checkpoint data at 10 from RAM and delete
reverse: forward advance to 11
reverse: adjoint step back to 10
reverse: load checkpoint data at 8 from RAM and keep
reverse: forward advance to 9
reverse: forward advance to 10
reverse: adjoint step back to 9
reverse: load checkpoint data at 8 from RAM and delete
reverse: forward advance to 9
reverse: adjoint step back to 8
reverse: load checkpoint data at 6 from RAM and keep
reverse: forward advance to 7
reverse: forward advance to 8
reverse: adjoint step back to 7
reverse: load checkpoint data at 6 from RAM and delete
reverse: forward advance to 7
reverse: adjoint step back to 6
reverse: load checkpoint data at 4 from RAM and keep
reverse: forward advance to 5
reverse: forward advance to 6
reverse: adjoint step back to 5
reverse: load checkpoint data at 4 from RAM and delete
reverse: forward advance to 5
reverse: adjoint step back to 4
reverse: load checkpoint data at 2 from RAM and keep
reverse: forward advance to 3
reverse: forward advance to 4
reverse: adjoint step back to 3
reverse: load checkpoint data at 2 from RAM and delete
reverse: forward advance to 3
reverse: adjoint step back to 2
reverse: load checkpoint data at 0 from RAM and keep
reverse: forward advance to 1
reverse: forward advance to 2
reverse: adjoint step back to 1
reverse: load checkpoint data at 0 from RAM and delete
reverse: forward advance to 1
reverse: adjoint step back to 0

The derivative calculation now alternates between forward + tangent-linear calculations, and adjoint calculations.

If we wished we could perform higher order adjoint calculations, using a binomial checkpointing schedule, by supplying a higher order tangent-linear configuration and differentiating the result.